玩个魔方
07-01
高二升高三暑假到了,以前从不报补习班的我,暑假时间被课程和作业排满。于是,魔方成为了最经济的娱乐方式。
还想多背一些CFOP…
改个标题,暑假想写点啥东西都写在这儿
07-05
又是个没有效率的一天。
在hosts屏蔽了一些网站。
07-11
你说的对,但《作业》是一款……
所以,做作业超过 5 小时为不健康时间, 累计经验值 损失 114514 点, 玩家愉悦指数 趋于$-\infty$…
作业这个东西不能欠的 还起来可难了 尤其在暑假 尤其在家里
07-13
呃 吃海底捞的时候带了本化学作业,一个服务员看到了拿起来翻了好久,这么想做就帮我做了吧
以前还有一次在地铁上写物理,当时在做光的干涉,好多基本的点都记不得,结果旁边一人死死盯着我写的字,还指出我有道题做错了。。
高手在民间啊
有时候不小心会用错:
如果题目中给出某个$f(x)$严格单调递增,则解$f^{′}(x)\geqslant0$得出单调增区间,再舍去一些肉眼可见的增根(常值函数之类)。若用$f^{′}(x)>0$则可能漏掉某些驻点。
课本还是很重要。翻了知乎没几个总结对的。
07-15
最近在翻九年级买的小猿搜题辅导书,看见一个构造法导数问题:
| 已知的不等式中所含结构 | 构造函数的方向 |
|---|---|
| $x^2f^{′}(x)+2xf(x)$ | $F(x)=x^2f(x),F^{′}(x)=x^2f^{′}(x)+2xf(x)$ |
| $xf^{′}(x)-2f(x)$ | $F(x)=\dfrac{f(x)}{x^2},F^{′}(x)=\dfrac{x^2f^{′}(x)-2xf(x)}{x^4}=\dfrac{xf^{′}(x)-2f(x)}{x^3}$ |
| $xf^{′}(x)-f(x)$ | $F(x)=\dfrac{f(x)}{x},F^{′}(x)=\dfrac{xf^{′}(x)-f(x)}{x^2}$ |
| $xf^{′}(x)+f(x)$ | $F(x)=xf(x),F^{′}(x)=f(x)+xf^{′}(x)$ |
| $f(x)+f^{′}(x)$ | $F(x)=e^xf(x),F^{′}(x)=e^x[f(x)+f^{′}(x)]$ |
| $f^{′}(x)-f(x)$ | $F(x)=\dfrac{f(x)}{e^x},F^{′}(x)=\dfrac{f^{′}(x)-f(x)}{e^x}$ |
| $\dfrac{f^{′}(x)}{f(x)}$ | $F(x)=\ln{f(x)},F^{′}(x)=\dfrac{f^{′}(x)}{f(x)}$ |
| $f(x)\cos{x}+f^{′}(x)\sin{x}$ | $F(x)=f(x)\sin{x},F^{′}(x)=f^{′}(x)\sin{x}+f(x)\cos{x}$ |
| $f(x)-f^{′}(x)\tan{x}$ | $F(x)=\dfrac{f(x)}{\sin{x}},F^{′}(x)=\dfrac{\cos{x}}{\sin^2{x}}\cdot[f^{′}(x)\tan{x}-f(x)]$ |
上海可能不常考,因为比较难想,并且教材中只涉及内函数是一次函数的复合函数求导。不过归根结底还是看公式熟悉程度,上海喜欢考的如,套点到直线距离公式的数形结合不等式题。
07-20
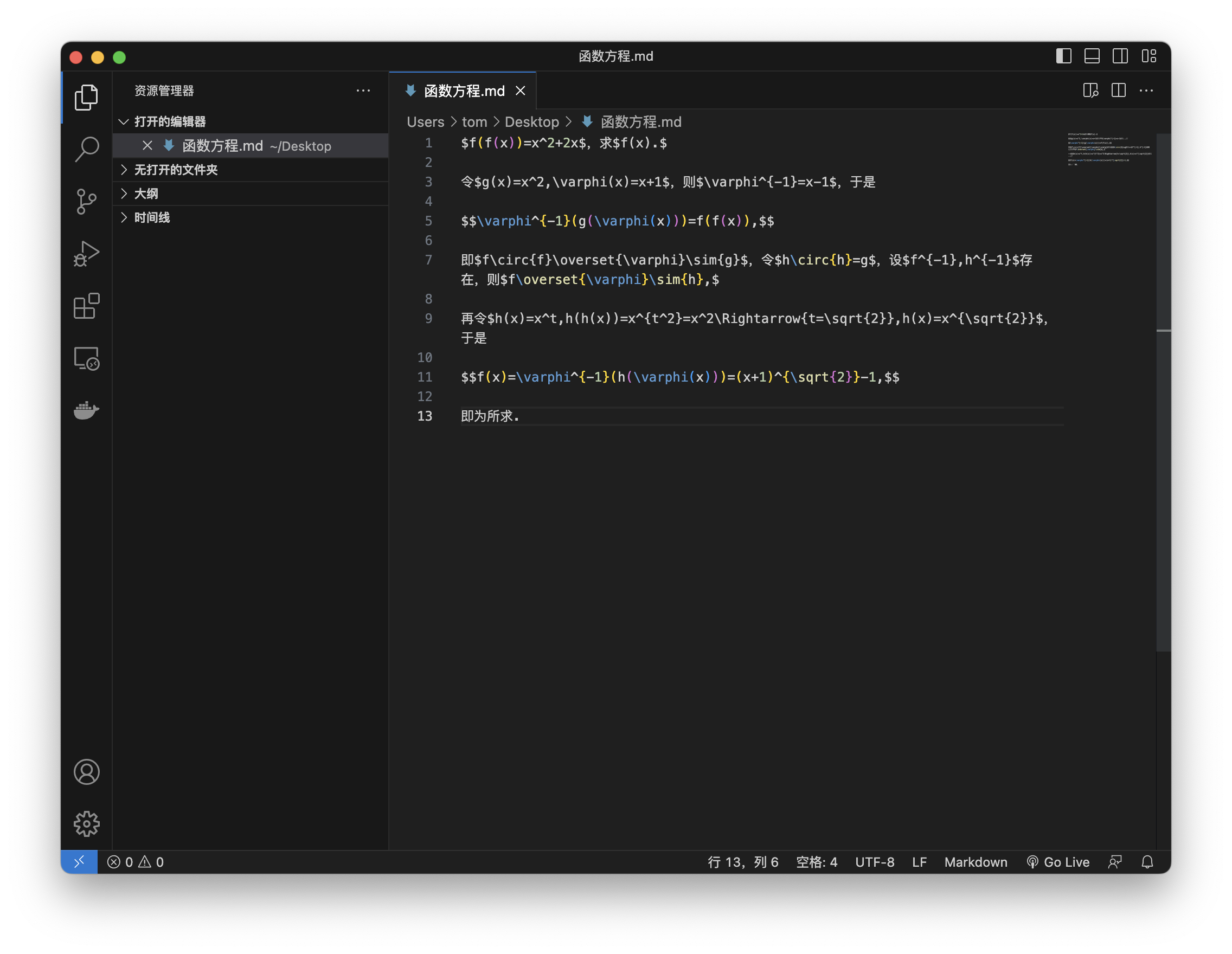
现有函数$f(x)$,使$f(f(x))=x^2+2x$,求$f(x).$
令$g(x)=x^2,\varphi(x)=x+1$,则$\varphi^{-1}=x-1$,于是
$$\varphi^{-1}(g(\varphi(x)))=f(f(x)),$$
即$f\circ{f}\overset{\varphi}\sim{g}$,令$h\circ{h}=g$,设$f^{-1},h^{-1}$存在,则$f\overset{\varphi}\sim{h},$
再令$h(x)=x^t,h(h(x))=x^{t^2}=x^2\Rightarrow{t=\sqrt{2}},h(x)=x^{\sqrt{2}}$,于是
$$f(x)=\varphi^{-1}(h(\varphi(x)))=(x+1)^{\sqrt{2}}-1,$$
即为所求.
(vscode新主题真的好看)
07-21
月底冲业绩!!!
07-25
百度这也是急了
手残的后果:误删的一个文件夹,花了一个小时处理
幸好有定时快照,恢复一下。
07-28
最近把博客中数学题目的展示效果进行优化,看起来已经不错了。以后会进一步改进。
07-29
高一的时候问过数学强基刘老师一个问题(那个老师还教过我一些抽象代数):
求:存在函数$f(x)$使得对于$\forall{m}\in{\mathbb{R}}$都有$f(g(m))=|m|$的充要条件.
老师给出的是“$g(|x|)$是单射”。之后有时间再好好研究一下,甚至看看能否推广。先占个坑。
07-30
参加一个“2023年普通高中学业水平模拟测试”的公益测试,考寄了。
07-31
啊 latex里cdots就可以打三个点啊。。我一直打三个cdot。。。
这作业是$真^{TM}$补不完啊……
08-01
这就已经八月了
08-02
终于整理排版好了近10年上海高考题(春考、秋考),总共大概20几份。。。
累到吐血
08-07
停更!
08-11
最近新听了许多曲子
不得不说,勃拉姆斯第一钢协是针不戳。
目前对听的钢协喜爱程度做个排序:
- 拉赫玛尼诺夫第三号
- 普罗科菲耶夫第三号
- 肖邦第一号
- 巴托克第二号
- 柴可夫斯基第一号
- 李斯特第一号
- 死之舞
- 勃拉姆斯第一号
- 肖邦第二号
- 莫扎特第十七号
- 贝多芬第一号
- 舒曼 A 小调钢协
- 拉赫玛尼诺夫第二号
排序第一的几首是听的最多的,40min的协奏曲随意抽一段我估计都能补出旋律,有时可能还有些新发现,比如注意到一些隐藏的声部(如拉三开头的小提琴声部,以前可能只关注到钢琴的主旋律)。并且拉三和肖协一的情感表达都十分有层次感。普三以其特有的活力感见长,而巴托克第二钢协的色彩丰富匈牙利风格、高难度的炫技以及极端不和谐的和声使其独树一帜,这两首初听都可能有些抵触,但在反复品味过后一定对此着迷。
第二和第三的一些协奏曲则主要以其旋律触动我,有些使我感觉似曾相识(如李斯特第一钢协),难道还在肚子中就听到过?
08-12
这道05年春考题还是比较有意思的,考了圆锥曲线的几何性质。当然第二问已经给出了方向,比如今的各种圆曲爆算和二级结论简洁优美得多。
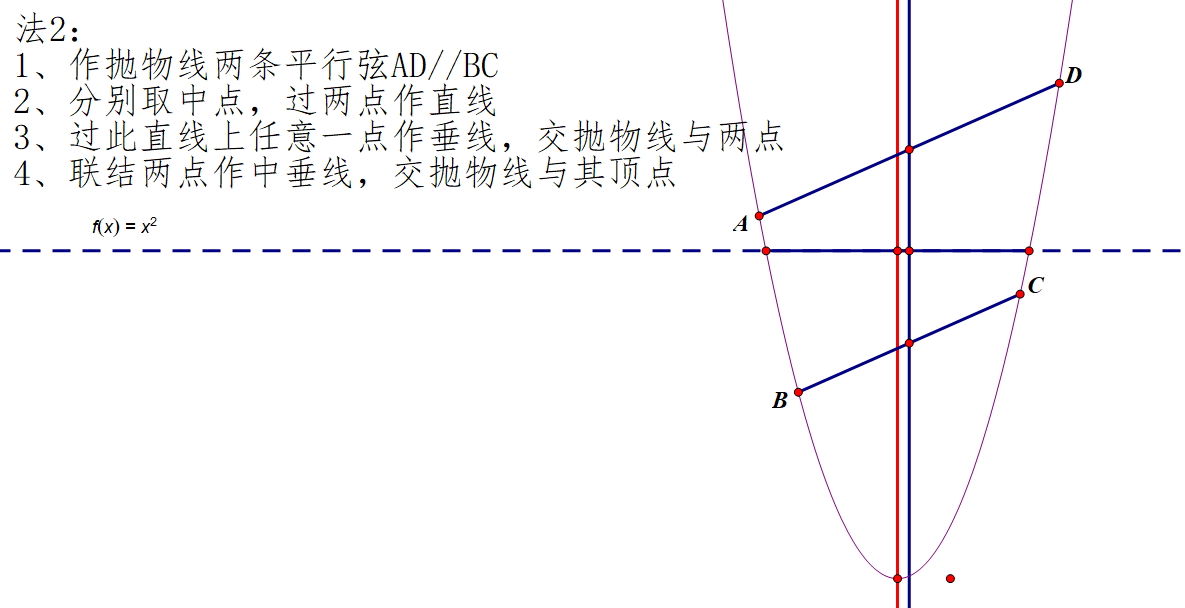
这题使我回忆起初三时,有一个预录七宝的同学谈及他在交附闵分面试的题目:尺规确定抛物线顶点。于是显然利用类似的几何性质。由于当时还是初三,不怎么了解圆锥曲线,只能拿几何画板凑,便凑出了如下方法:
这个法2便是05春考涉及方法。当然作为自招面试题未免太难为初中生,但还是能够考察一定的思维能力,比如“先猜后证”。
升高一那个暑假真是卷啊……
08-13
头痛。。。
08-18
课题怎么整
徐汇一模12怎么还考将军饮马 哭
08-20
用微信就一定要关闭个性化推荐。方法:
- 设置 - 个人信息与权限 - 个性化广告管理 - 关闭
- 视频号 - 隐私 - 个性化推荐 - 关闭(2项)
- 看一看 - 设置 - 个性化推荐 - 关闭
- 公众号 - 设置 - 个性化推荐 - 关闭
目前还没有多少人能抵抗来自机器算法的个性化推荐,除非有强大的意志力,否则会眼看着自己迷失在无意义的短视频与图文中。
假期已经过得只剩一周时间了,根据两个月以来的经验感觉也做不了什么事情了….
但希望能用对待国庆七天假的心态好好利用。
为了避免开学考阴沟里翻船,还是需要再感兴趣上的学科多克制,而努力面对自己不想看到的事物。。。
cml说高三是一场马拉松,不能一开头就用百米赛跑的速度。即将的开学要注意适应调整,达到最佳状态。
高三加油!